Shapes lesson 3: Properties and types of triangles and quadrilaterals

Practice problems. 

1. Give some examples of properties of triangles that don't change if you make the triangle bigger or smaller or turn it on its side.

• Angles don't change, so being obtuse (one angle more than 90°), right (one right angle), or acute (all angles less than 90°) doesn't change if you make the triangle bigger or smaller or turn it.
• The number of sides that are the same length doesn't change, so being scalene (no sides the same) isoscles (at least two sides the same) or equilateral (all sides the same length) doesn't change with the size and orientation.
• You could also describe other things about angles--for example, having an angle that is 45° doesn't change with the size or orientation of the triangle.

2. Make sure you can draw, identify and/or make on a geoboard grid triangles in each of the categories where it's possible to make such a triangle.

	Acute	Right	Obtuse
Scalene
Isosceles
Equilateral	Equilateral triangles can't be made on a geoboard	not possible to make	not possible to make

3. Which special triangle is it impossible to make on a geoboard? Equilateral

4. What's wrong with saying the length of this side of the triangle (the one on the right) is 2? A geoboard unit is the space between adjacent horizontal or vertical spaces. Diagonals spaces between pegs are larger then vertical and horizontal spaces, so this is longer than 2 (horizontal or vertical) spaces. 5. What's wrong with saying the length of this side of the triangle (the one on the top) is 5? Lengths are always measured by the number of spaces, not the number of pegs, so this is only 4 units long.

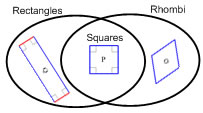
6. What are some other names besides "square" that are correct for shape P? P is also a rectangle, a rhombus, a parallelogram and a quadrilateral.  (Make sure you have rectangle in your list--that's the trickiest one) 7. What are some of the other names besides "rectangle" that are correct for shape Q? Q is also a parallelogram and a quadrilateral.  (Make sure you didn't call it a square).

8. What is a rhombus? A quadrilateral with all equal sides.

9. What is a parallelogram? A quadrilateral with 2 pairs of parallel sides.

10. What is a trapezoid?  A quadrilateral with 1 pair of parallel sides (or one and only one pair of parallel sides, or at least one pair of parallel sides)

11. Draw 3 different shaped examples of trapezoids.

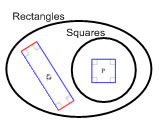
12. Draw a set (Venn) diagram that shows how squares and rectangles are related.

13. Draw a set (Venn) diagram that shows how rhombi and parallelograms are related.

14. Draw a set (Venn) diagram that shows how rhombi and rectangles are related.