
Big ideas:
Open this link in a new tab or window (wait for a few minutes--it will take a while to load) and experiment with the shapes by dragging the vertices (dots) that are not black.
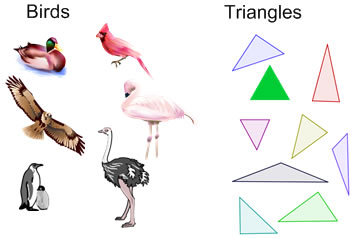
You should notice (and it shouldn't surprise you) that you can drag the 3 vertices of the triangle anywhere--triangles have very conditions--if you pick any 3 points that are not on the same line, you can make a triangle. Being a triangle is more like being a quadrilateral than it is like being a rectangle or a square. Rectangles are more like each other than triangles are like each other, and squares are even more alike than either triangles or rectangles.
This makes teaching "triangle" "rectangle" and "square" tricky in a very subtle way. Children need to know that you can have lots of different side lengths and angles in a triangle, but if it's a square then all of the sides have to have the same length, and all of the angles have to be right angles. It's pretty tricky that we learn/teach squares and triangles together, but there are so many more different kinds of triangles than there are squares.
| The word "triangle" is like the word "bird" because there are a lot of different families and species of birds, and they're all considered birds. Likewise, there are a lot of different combinations of side lengths and angles that all make a triangle. |  |
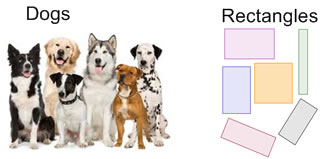
| The word "rectangle" is more like the word "dog". Dogs are more of a kind than mammals--it's only one species, but there are still a lot of different breeds of dogs. |  |
| If the word "rectangle" is like the word "dog" then the word "square" is something like the word "German shepherd". I pick this analogy because (1) German shepherds are a breed of dog that all look a lot alike--kind of like squares, and also because (2) German shepherds are dogs, and one of the trickier things about rectangles and squares is that squares are one specific kind of rectangle. |  |
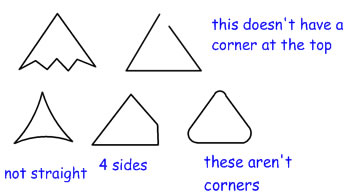
| When children learn the word "triangle" they often are learning it from a single picture of a triangle or a small number of different triangles. This results in the misconception that triangles have to not only have 3 sides and 3 angles, but also have to have the sides be about the same length and often children will believe that triangles have to have its flat side on the bottom, and point at the top, and it has to look like a tooth or a witches hat. When presented with a variety of triangles, they may believe that only the point up equilateral triangle is really a triangle, and that the other 3-sided shapes are not triangles because they are too different from the standard equilateral triangle. | 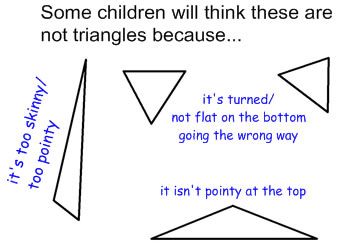 |
PreK-K teachers can help avoid this misconception by using examples of several different shaped triangles when teaching about triangles and shapes It's also good to work with manipulatives and pictures of triangles in different positions so that children get used to seeing triangles turned a different way from having a side horizontally on the bottom |
 |
| It's an advantage to address this particular misconception as early as possible, because once children internalize a definition of triangle, it's hard to correct that idea--if you're encountering this misconception in children at second grade or above, then it tends to take many exposures and corrections to replace the old idea with a new idea | |
| Another misconception that children often have about triangles is to accept approximate triangles because the overall shape looks triangular. One explanation for this might be that they are used to accepting as a triangle something that they or a classmate drew when intending to draw a triangle, but that had some flaws. This is a rather different misunderstanding, and needs a different sort of teaching approach | 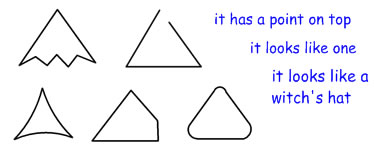 |
The key thing to understand this better is to practice looking for properties: count the sides, count the corners
|
 |
| Looking at properties can help in higher grades (1+) with understanding that triangles can have different shapes. Being able to put a name to the triangle that fits your mental picture (equilateral) and naming the triangles that don't fit your mental picture but are still triangles, helps with creating the mental space for all of the different possible triangle shapes. | 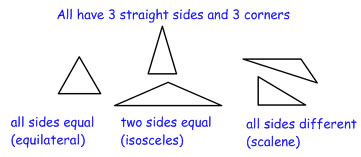 |
Sometimes children have rigid ideas of what a rectangle is: that a rectangle has to be roughly the shape of a door to be a rectangle and if it is too fat or too skinny or tilted then it's not a rectangle. Usually, though, the main misconception about rectangles is that the length and width of a rectangle have to be different (they don't). |
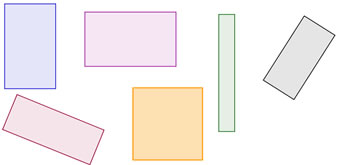 |
| Now, of course, children believe that the length and width of a rectangle have to be different because they've been told that they have to be different. Almost always when explaining the difference between a square and a rectangle, we tell children that squares have the same sides, and rectangles have different sides. It's fairly natural, because it's easier to explain than the more mathematical relationship that says that squares have to have the same sides and rectangles can (but don't have to) have different side lengths. And, of course, it fits the pictures in your kindergarten classroom. | 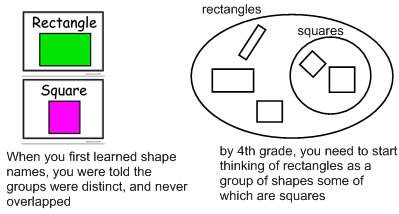 |
| It's not just that it's easier to explain what a rectangle means if you say that the length and width are different, it's also an acceptable English language usage and definition. If you check the dictionary, you'll find both definitions: the one where a rectangle has to have different side lengths and the one where it can but doesn't have to have different side lengths. Usually, you learn the first definition in kindergarten, but you need to know and be able to use the second definition in 4th grade. | 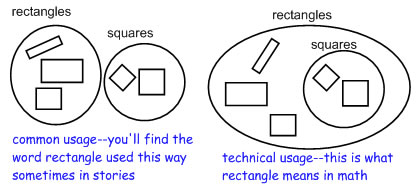 |
| So, to indulge my metaphor again,learning about rectangles and squares isn't so much like learning about dogs and German shepherds, it's more like learning about tomatoes and fruit. If you cook with it, then you think of a tomato as a vegetable and not a fruit, but if you study it in biology, then a tomato is definitely a fruit. At some point, if you're going to learn more about fruit and tomatoes, you have to change your mental definitions so that tomatoes are fruit. At some point, if you're going to learn more about math and geometry, you have to change your mental definitions to include a square as a special kind of a rectangle. |  |
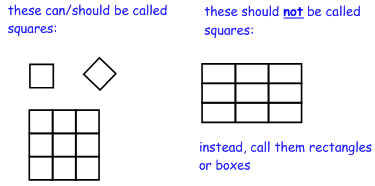
I'm not going try to insist that you to teach rectangles differently in kindergarten (though I want you to be aware of the problem). I do, however, want you to be careful with your language going the other way. Please don't call rectangles squares. You can call them boxes if you want a smaller word, but it can really make a mess of a problem if, when you hear the word square, you think rectangle and not square. |
 |
One of the key things that children should be learning about shapes in the primary grades (according to CCSS) is to distinguish defining properties of simple shapes from other properties the shapes may have.
For instance the properties that are usually used to define triangles, rectangles and squares are:
| Triangle | Rectangle | Square |
3 straight sides |
4 straight sides |
4 straight sides All sides are the same length 4 vertices All corners are right angles |
There are other properties that these shapes also have that can be considered defining properties. To be a defining property, it has to be a property that the shape always has, and must have in order to be considered that shape.
| Triangle | Rectangle | Square |
3 straight sides |
4 straight sides |
4 straight sides |
There are lots of other properties that a shape can have that aren't defining properties. A shape can be any color or tilted at any angle and that doesn't change what shape it is. These are characteristics that most children pick up fairly easily are not defining characteristics. The tricky part comes in when you're asking about properties that children sometimes have erroneously in their mental image of that shape, but that aren't really necessary for the shape.
| Triangle | Rectangle | Square |
A triangle can be any color--color doesn't change whether it's a triangle or not. |
A rectangle can be any color--color doesn't change whether it's a rectangle or not. |
A square can be any color--color doesn't change whether it's a square or not. |
So, our goal for teaching shapes, as much as possible, is for children to have mental images and understood definitions of the basic shapes that will be the definitions they will need to know later as they study geometry. Children should understand the varieties of shapes that are all considered triangles, and should understand varieties of rectangles in a way that will make it easy for them to understand the subset relationship between squares and rectangles at the point when they will be studying that (CCSS places this explicitly in 5th grade).