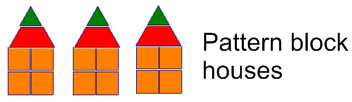
1. If you have an ABC pattern, how many tiles (at least) should you show so that children can figure out and be confident they know what the pattern is?
at least two full repetitions
2. Which of these questions are appropriate for kindergarten children, when asked about an ABC pattern where 9 tiles are shown and the next 6 are hidden (and the visible and hidden tiles are numbered)?
a. What comes next in the pattern?
b. What are the next 5 tiles in the pattern?
c. What is the 14th tile?
d. What is the 20th tile?
e. What is the 100th tile?
a, b and c are all physical tiles under physical cups and therefore accessible to kindergarten aged children.
3. Write a 3rd grade question or problem about the pattern described in #2 that suggests a skip counting strategy.
Example: What numbers are under the first 8 "A" tiles?
Acceptable variations: ask about B or C tiles. Ask for a different amount of numbers (though the amount of numbers should be greater than 6, since 6 is only one more than the tiles that are physically available).

4. Write a problem or set of problems that use the multiplicative nature of this pattern.
Example: How many tiles would it take to make 6 houses?
This problem could be usefully preceded by a question about how many blocks are in one house. Asking about any number of houses 5-10 would be appropriate numbers of houses to ask for--any fewer than that would not be likely to encourage a multiplicative strategy.
Alternate example: how many orange squares would it take to make 6 houses?
Note: a question about the number of trapezoids or the number of triangles would not be considered multiplicative, since there are only one of each per house.
5. Write an easier and a harder set of problems that use the ratio relationships between different kinds of pattern blocks.
Easier example: If I used 7 triangles making houses, how many squares would I need?
Harder example: If I use 20 squares making houses, how many trapezoids would I need?Notes: In the easier example, I tell a number of shapes (triangles) for which there is only one (triangle) in each house, so telling that number (of triangles) is equivalent to telling the number of houses. The problem can be solved readily by multiplying.
In the harder example, I tell a number of shapes (squares) for which there are several (4) per house, so to solve, you would need to divide the total number of such shapes (squares) by the number (or squares) in each house.
If this were a pattern where there were two triangles and 4 squares per house (for instance) a question about the relationship between triangles and squares would be even harder, since it might be seen as involving both multiplying and dividing.
6. Write a question about possible houses that relies on an understanding of how the number of square pattern blocks corresponds to the number of houses.
Example: Can I make a street of houses using 19 squares?
Note: this problem relies on students recognizing that the number of squares must always be a multiple of 4 (or at least that it must always be even)?
The following questions refer to the pattern block fish pattern:
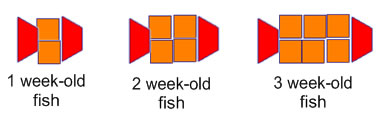
7. In what way is this pattern more complicated to understand than the houses pattern above?
This pattern has both a multiplicative part (the squares) and an additive part (the trapezoids).
8. Write a problem or set of problems to help children analyze and understand the pattern of the growing fish.
Example 1: Build a 4-week old fish
Example 2: What changes when the fish gets older? What stays the same as the fish gets older? How many more blocks are in the 3-week old fish than the 2-week old fish? What kind of blocks are added?
9. Write a problem or set of problems to help children gather and organize information about the fish pattern.
Example 1: Make a table with the age of the fish, how many trapezoids you need, how many squares you need, and how many total pattern blocks you need for the fish.
Example 2: How many trapeziods are there in a 1-week old fish? 2-week old? 3-week old? How many would you need for a 4-week old fish?
How many squares are there in 1-week old fish? 2-week old? 3-week old?
How many squares would you need for a 4-week old fish?
10. Write a problem or set of problems asking children to make 3rd grade appropriate predictions about the growing fish pattern.
How many pattern blocks would you need in all to make a 5-week old fish?
How many blocks would you need for a 10- week old fish?
How many blocks would you need for a 20-week old fish?
How can you figure out the number of blocks you will need before you build the fish?
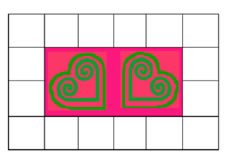
11. Which of these patterns (there may be more than one) will make a completed pattern for this border?
a. rb b. rrb c. rrbb d. rrbbb
Explain how you know. Patterns a and c will be complete. This border mat has 16 squares. To make a complete pattern, a unit pattern has to have a length that divides evenly into 16. 2 and 4 are both factors of 16, so they will make completed patterns. 3 and 5 are not factors of 16, so they will not make completed patterns.
12. What is the longest border pattern you could make that would be complete in this border, and that would show the pattern at least twice on the border mat?
Besides 2 and 4, the only factors of 16 are 1, 8, and 16. A pattern of length 16, would not show any repetitions, so the longest pattern that would show a repetition would be a pattern of length 8.
13. The pattern ABCABC is exactly the same pattern (will look exactly the same) as:
a. ABBABB b. ABC c. ABCA d. ABCAB e. CABCAB
It is exactly the same as b. ABC, because if you do ABC twice you get exactly ABCABC.
The other answer that is closest to being correct is e--if you rename the letters, this is exactly the same, so the pattern has the exact same structure (though it's not the exact same pattern in the way that b is).
a, c and d are definitely not correct: ABB anc ABC are different; ABCA when it repeats goes: ABCAABCA, with two A's together, which you don't get in an ABC pattern.
14. Fill in the blanks to make the sentences correct:
a. __3__ is a factor of __15__ (15, 3)
b. __36__ is a multiple of __4____ (36, 4)
c. __27__ is divisible by ___9____ (27, 9)
d. __42__ can be evenly divided by __6__ (42, 6)
e. __7__ divides evenly into _56__ (7, 56)