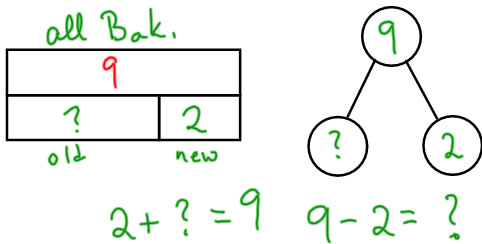When children start solving addition and subtraction problems, their strategies tend to be context specific--that's what the CGI difficulty levels and problem types analyze: how do children analyze the problems, which do they think of as more difficult, and how do they go about solving them?
As children get older (second grade, perhaps late first grade), it's important that they make connections between different problem types. In particular it's very helpful for children to make the connection between addition and subtraction, so they can use addition strategies and facts to figure out subtraction problems. One way teachers can help with this transition is by using part-whole language to describe both addition and subtraction situations. In this lesson, we're going to look at 2 types of diagrams that help with making that connection to thinking of all addition and subtraction problems as part-whole relationships:
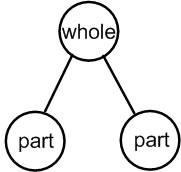
This is sometimes called a part-whole diagram, and sometimes called a bar diagram. It should look familiar because we get basically that same picture if we solve an addition problem with linking cubes, and we snap the cubes together, or if we solve the problem with Cuisenaire rods. These diagrams are particularly useful for Part-Part-Whole and Compare problems, and relating those kinds of problems with Join and Separate problems. |
 |
| This diagram is sometimes called a number bond diagram, and is sometimes called a math mountain. This kind of diagram is particularly useful for showing Join and Separate problems (the lines in the number bond imply an action), and can be used to relate Join and Separate problems to Part-Part-Whole problems. Number bonds don't work as well for Compare problems. |  |
The basic examples of how these diagrams are used are for part-part-whole problems:
PPW-WU There are 8 green Jolly Ranchers in my pocket, and 10 purple Jolly Ranchers in my pocket. How many Jolly Ranchers are in my pocket? When discussing this problem, we first identify the parts: the green and purple Jolly Ranchers, and the whole: all the Jolly Ranchers. We can add curly brackets to the part-whole diagram to make room to label the parts and wholes with a description as well as the numbers. A typical teacher-drawn diagram will indicate the unknown somehow: I've gotten in the habit of marking the unknown with a question mark, but it could be left blank, or a line put there to show where the solution will go. |
Because the whole is unknown, the best number sentence for solving this is an addition number sentence: 8+10=? |
PPW-PU There are 14 T-shirts in the drawer. 5 of the T-shirts are white and the rest are blue. How many of the T-shirts are blue? First identify the parts: white and blue T-shirst, and the whole: all T-shirts, and label the diagram with the known numbers and mark or discuss the unknown. Then discuss different ways of seeing the problem: we can think of is as subtraction or unknown addend addition |
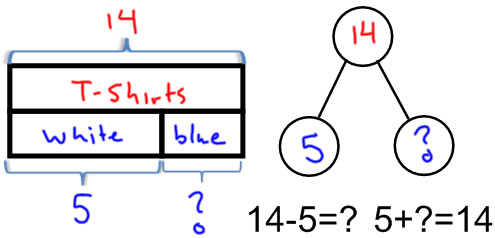
The two number sentences are really important here. Understanding that subtraction can be solved as a unknown addend addition problem is a key goal for this work. |
When we look at the CGI problem types, JRU is easily identified with PPW-WU (this happens naturally as children gain experience with PPW-WU problems). The subtraction problems are harder to connect to the part-whole model, so that's where discussion and and instruction is the most valuable.
The main goal of using Part-Whole language and diagrams for addition and subtraction is to help children:
More examples:
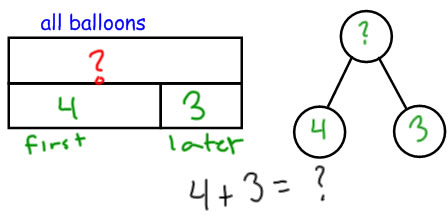
JRU Sam blew up 4 balloons. Later he blew up 3 more balloons. How many balloons did he blow up in all? This is probably the easiest problem type to associate with a part-whole diagram |
 |
JCU Gwen wrote 1 poem. How many more does she have to write to have 4 poems? |
 |
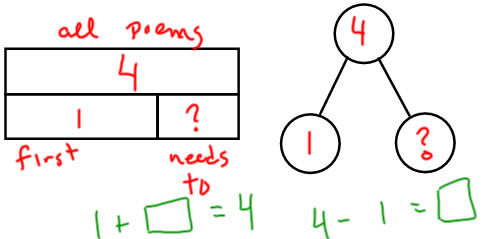JSU Sam had some Bakugans. For his birthday, he got 2 more Bakugans. Now he has 9 Bakugans. How many Bakugans did he have before his birthday? Note: for all of the Join problems, the result is the whole, and it is made out of the part that was had first, and the part that was added. |
 |
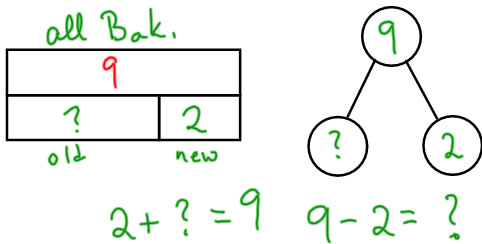SRU Gwen had 12 markers. 4 of her markers dried out. How many markers did she have left? Here, we describe the whole being separated into two sets--the part that dried out and the part that was left. |
 |
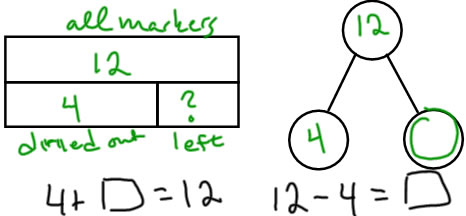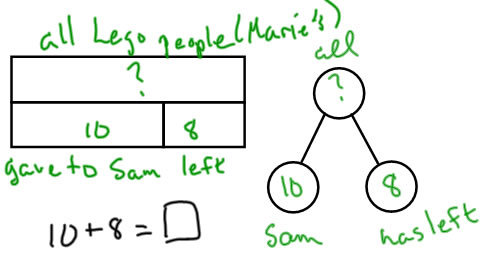
SCU Marie had some Lego people. She gave 10 Lego people to Sam. Now she has 8 left. How many Lego people did Marie have to begin with? |
 |
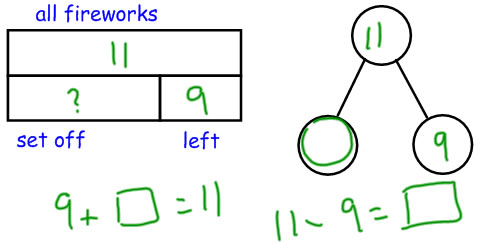SSU Marie had some Lego people. She gave 10 Lego people to Sam. Now she has 8 left. How many Lego people did Marie have to begin with? Note: Making the part-whole diagram for SSU shows clearly that the problem can be solved by addition (easy), whereas the natural number sentence that comes from the separate context: Note: For all of the separate problems, the whole is what is started with, and it is separated into two sets: the amount taken away, and the amount left. |
 |
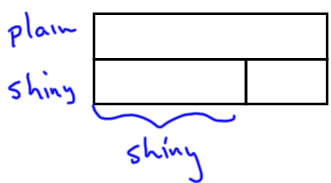
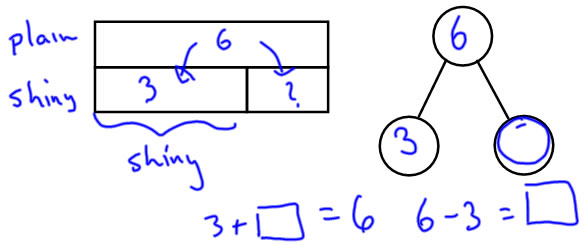
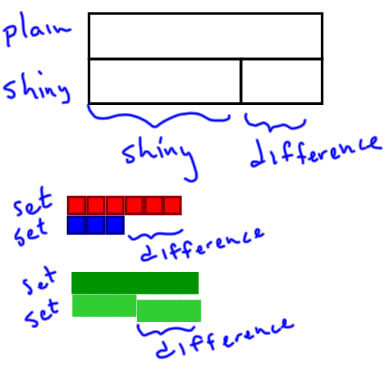
CDU: Jeff has 3 shiny stickers and 6 plain stickers. How many more plain stickers than shiny stickers does Jeff have? Note on Compare problems: For compare problems, the first thing we do is different, because there isn't an obvious whole. What we identify first is which sets are compared and which is the larger of the compared sets. So, the first thing I do is to label the bars with the set names: the larger set is labelled on the long "whole" bar, and the smaller set is labelled on a short "part" bar. Notice that the bar diagram version is very similar to what you see with counters or Cuisenaire rods for modeling compare problems. To make the connection to part-whole ideas, we notice that the larger set can be split into two parts: one part is the size of the smaller set, and the other is the size of the difference. |
|
CQU Ethan has 8 green bouncy balls. He has 1 fewer blue bouncy ball than green bouncy balls. How many blue bouncy balls does he have? Notice: that whether we think of the bar diagram as a compare diagram or a part-whole digram, it lets us write both a subtraction and a unknown addend addition equation that would let us solve the problem. |
 |
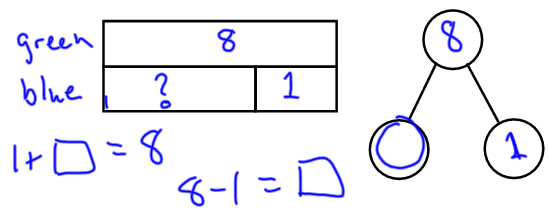CRU Jill has 7 green bouncy balls. She has 2 fewer green bouncy balls than blue bouncy balls. How many blue bouncy balls does she have? Note: In compared problems, we determine which set being compared is larger. The larger set can be partitioned into a part the size of the smaller set and a part the size of the difference, so the larger set is the "whole" and the smaller set and the difference are the parts. |
 |
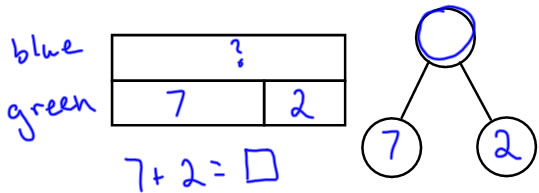