As with use doubles, make 10 is a derived facts strategy. That means children need to know some facts by hear before they can use a make 10 strategy.
The key facts for using a make 10 strategy are 8+2=10 and 9+1=10, but there are also other facts and skills you need, so usually children are ready to learn the use doubles strategy before the make 10 strategy.
An example of the make 10 strategy is when adding 8+5, you use that 8+2=10, and decompose 5 into 2+3. Then you group the 2 with the 8 to get 8+5=(8+2)+3=10+3, then add 10 and 3 to get 13.
There are 3 different category of math facts in use here:
Decomposing a number into 1 or 2 and some more is a skill that's learned with number decomposition tasks and games (like those discussed in the lesson on fluency with small numbers), and it's learned in practicing subtracting 1 and 2 from a number.
Adding a 1-digit number to 10 is a skill that's learned along with base 10 concepts and skills.
Decomposing 10 is probably the last skill that is learned in this set, though the most commonly used facts 8+2=10 and 9+1=10 are, of course, easier than the others.
While the make 10 strategy is most efficient when adding a number to 8 or 9, the strategy of making tens when adding is so integral to working with our number system, that learning all of the partners that make 10 is a valuable skill. To learn these number partners it helps to spend time working with a material where children are expected to subitize values, and where the material naturally compares values to 10.
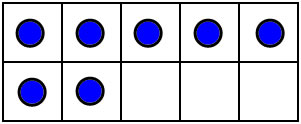
10-frames are good for learning partners that make 10. When building or looking at a number on a 10-frame a natural question to ask is--how many more are needed to make 10? For example, in this 10-frame showing 7, the same subitizing pattern for 3 shows that the amount left to make 10 is 3.
Rekenrek: Another good material for 10's is a Rekenrek. When made with just one string, this is sometimes called a bead string, and when made into a whole 100-abacus it is sometimes called an ALAbacus or a Slavonic abacus.
Here is a bead string showing 7, and you can see that the complement of 7 to make 10 is 3 by looking at the other end of the string
You can check out some virtual Rekenreks on line here and here.
10's go fish: Finding partners that make 10 can also make a good go-fish game. Play go fish in the usual way, except that instead of looking for 4 of a kind, you are looking for 2 cards that add together to make 10 (so you need 4 each of the number cards 1-9, or, if you have a deck with 0's, 0-10). I suggest starting with 5 cards each. The most learning happens when the child is deciding what card to ask for: you must ask for the card you want, so if you have a 4 in your hand you need to figure out that 4+6=10 and ask for a 6.
The make 10 strategy is also called the bridge through 10 strategy. It can be used whenever the sum is more than 10, though it's easies to use if one of the addends is 8 or 9.
To use the make 10 strategy, the child recognizes that one of the addends is close to 10, and if you add on the other one, you will get more than 10. Then the child decomposes the other number so that they can turn the sum into 10 and some more.
Representations
It's a good idea to have some ways of representing the make 10 strategy. Manipulatives and diagrams to clarify the make 10 strategy are a very good idea. Here are some ways to show the make 10 strategy with some appropriate materials.
With 10-frames
For example, to figure out 8+5, we realize that 8+2=10
Then we partition 5 into 2+3, and take 2 from the 5 and give it to the 8 to make 10. This leaves us with 10+3:
So the sum is 13.
Rekenrek
You can show the same thing on a 2-bar Rekenrek by sliding beads back and forth:
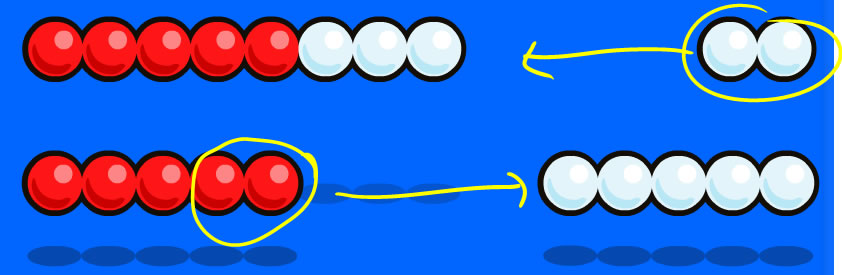... becomes...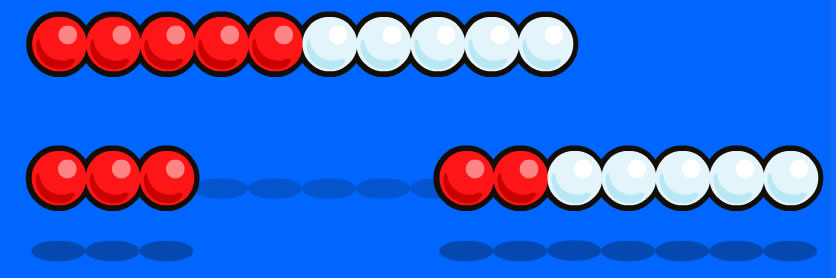 
Cuisenaire rods
Sometimes it helps to sandwich the 8 or 9 between two 10s to make it clear what you're trying to acheive:
So we have 8+5, and we have the 8 sandwiched in between 10 rods, so we can see the space we need to fill to make 10.
We split the 5 into 2+3 so we can fill the spot between 8 and 10, so we get 8+2+3
And finally 10 and 3 is 13.
An open number line is a very good way of showing the make 10 strategy for adding:
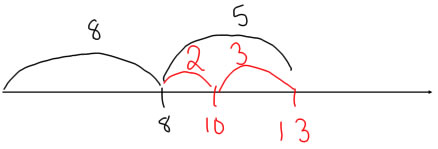
Being an open number line means that instead of writing onto the number line all of the numbers before you start, you write on just the ones you need in order to keep track of what you are doing. This number line diagram shows 8+5, and of course, the jump to 8 lands at 8, but it's not obvious where the jump of 5 will land. To figure that out, you have to break 5 into 2+3. The jump of 2 lands you right on 10, and jumping 3 from 10 lands you at the sum of 13.
Make 10 is considered a fast efficient strategy when the sum is more than 10 and one of the addends is 8 or 9. It isn't considered efficient for other sums largely because of the need to decompose the second number. Decomposing any number into 1 or 2 and some more is easier than the other decompositions, and if, for example, you wanted to use the make 10 strategy for 7+5, you would be using 7+3=10, so you would need to decompose 5 into 3 and some more, which is harder to visualize than decomposing 5 into 2 and some more (even though it's exactly the same decomposition). Make 10 can be used for any problem where the sum is more than 10, though it may not be considered efficient.
Sample make 10 lesson with word problems
The teacher reads the problem:
Jacob has 9 paper airplanes. He makes 6 more paper airplanes. How many does he have now?
The teacher waits while the children solve the problem, and then invites children to share how they solved the problem.
If a child explains a make-10 solution, then the teacher highlights that solution at the end. Something like: "there were a lot of ways to solve that problem. Does anyone remember how Jeremy solved it? [invites another child to explain Jeremy's make-10 solution]. Then follows up "so Jeremy took 6 and split it into 1 + 5, and put the 1 with the 9 to make 10. I have another problem with the number 9 in it". [The teacher illustrates the strategy using a familiar material--10-frame, number line, etc.] The teacher then invides the children "See if you can use that same trick of making 10 to solve this one:
Sarah has 9 flowers. Amy has 4 more flowers than Sarah. How many flowers does Amy have?
The teacher waits while the children solve the problem, and then asks: did anyone make a 10 when they solved this problem? [the teacher invites a child to explain how they made a 10 to solve the problem].
If no child offers a make-10 solution after the first problem, the teacher might ask some questions:
Alternately, the teacher might say:
I remember seeing someone solve this problem once a different way. What they did was to take one of the 6 and add it onto the 9 to make 10, and then they figured out that the rest of the 6 would be 5 more, and so then they just did 10+5 to solve the problem.
Again, the teacher illustrates the strategy with a familiar material, such as those just discussed, and then goes on to the second problem as before.
Thoughts about problem types:
I've used JRU and CQU as my problem types for these problems. JRU is closely associated with counting on, so that's a negative for encouraging some strategies. Make 10, however, is a modified version of counting on--it's an adding on strategy. Specifically, you start with one addend and add on enough to get to 10, and then you add on the rest. Adding on is just a more efficient version of counting on, so it's hard to come up with a good problem type for make 10 that isn't also a good problem type for counting on.
Thoughts about numbers
Eventually, children should solve problems where one addend is 8 or 9, and later still, children may learn making 10 with smaller addends. To begin with, however, its easiest to see what to do if the first addend is 9--as close to 10 as you can get without actually being 10. It's also good to begin with a moderately large number for the second addend (6 is a better choice to start with than 4... indeed, 4 may be too small even for the second problem--maybe I should go back and change it to 7) because you want to make it not too tempting to count on.
If children know all of the partners that make 10, they can sometimes use them to solve problems where the sum is near 10. This strategy is very similar to the use doubles strategy. For example, if a child knows that 6+4=10, then they can figure out that 6+3 is one less than 10, so 6+3=9. This is different from the make 10 or bridge through 10 strategy which refers to converting a sum to a sum of 10 and some more. Use 10 is generally not emphasized as much as a strategy because it applies to a lot fewer problems than does the make 10 strategy.
Summary
In order to use the make 10 or bridge through 10 strategy, children must:
The best manipulatives for learning the sums that make 10 are those which show numbers in a way that can be subitized, and show their relationship to 5 and 10. Three examples of this are 10-frames, bead strings (Rekenreks), and fingers.
(10's go fish is a fun game)
The steps in a make 10 is a strategy are (example 9+7)
Make 10 can be shown and explained efficiently with two 10-frames; with a 2-bar Rekenrek or with an open number line.
Make 10 is a strategy that can be applied any time the sum is greater than 10, and the addends are less than 10.
Make 10 is is an efficient strategy for problems where the sum is greater than 10 and one of the addends is 8 or 9.
Bridge through 10 is another name for make 10
Use 10 is a different strategy that uses knowledge of partner numbers that make 10 to solve problems where the addends are close to partners that make 10.
