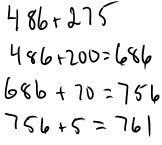
The traditional algorithm that we learned in school has some great advantages--it's compact (you can fit your work on a small amount of paper); it shows all of the important steps (you can look back later to see what you did at each step); it's thoroughly de-bugged (people have been using this for a long time, and there aren't any hidden problems with it) and it's what most people use (when someone else looks at your work they will know right away what you did and how you did it--no communication problems).
The traditional algorithm, however, doesn't always fit the way that children think. Using manipulatives to work through the steps helps make the standard algorithm make sense to children, but there are other approaches that have other advantages too. If you teach addition and subtraction through asking good problems and asking children to solve the problems in ways that make sense to them, children will come up with a range of strategies and ways of recording those strategies. Spending time developing childrens ideas is often time well spent in terms of children getting a robust understanding of how addition and subtraction works and what it represents. If you teach by questioning and problem solving you'll see a lot of different ideas and strategies that children come up with.
Even if you are teaching the traditional algorithm, there will be some children who come up with their own ways to add and subtract that work and make sense. It's important as a teacher to be able to look at work that children do, and recognize it as a valid alternate strategy that works and makes sense, or to recognize that it doesn't work, and figure out what the problem is with the strategy. It's discouraging for a child to use an alternate strategy that works (one they made up, or one they learned from a parent who grew up with a different school system) and be told that the they're wrong because they did it a different way. Even if we eventually want children to be able to all add and subtract using the standard algorithm, it's important to be able to recognize and praise correct thinking.
The other situation where learning other algorithms can be useful as a teacher is that there are some alternate ways of adding and subtraction that are sometimes used as a teaching strategy for children who aren't ready for the standard algorithms.
Universal student invented algorithms:
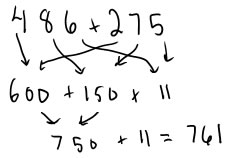
Universal algorithms are ones that work for all problems, with all numbers. Algorithms for addition (efficient ones that use place value) always have some version of adding numbers in their place value, and then combining the numbers. The combining can be recorded in different ways and happen in different orders. Here are two examples:
 |
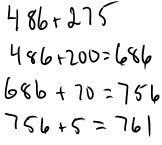 |
The version on the left is just a way of recording that the student adds in each place value (hundreds, tens and ones) and then adds those sums one at a time. The second is an algorithm that's most often used for mental arithmetic, where the place values of the second addend are added one at a time to the first addend. In both cases, children are adding within the place values, but in the version on the left, the place values are added first and then combined, and in the second, the sums are combined in each step.
Alternate algorithms for teaching: The expanded algorithm
The one algorithm that's sometimes useful to teach to students that's not the standard algorithm is the expanded algorithm. It's called the expanded algorithm because it's similar to the standard algorithm, but it takes up more space (it's expanded) and is easier to understand. Algorithms like this are often used as an intermediate step to teaching the standard algorithm--the way they are written down is similar to the standard algorithm to make it easier to learn the standard algorithm later. The expanded algorithm is a vertical way of writing down the first example of student invented algorithms:
One advantage of the expanded algorithm over the standard algorithm is that it works equally well left to right or right to left. This makes it a particularly good trick to have available to you as a teacher for using with children who freqently make mistakes by trying to use a left to right order with the standard algorithm. The expanded algorithm involves adding each place value in columns and then adding the partial sums.
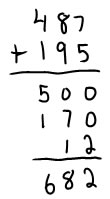
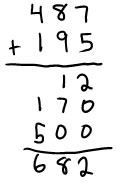
Friendly numbers strategies (round and compensate and make ten):
Some strategies work only if you have nice numbers. If numbers are quite close to tens or hundreds, you can round to the nearest ten or hundred and then add or subtract to compensate. Compensating when you are adding is pretty easy because the addends play the same sort of role. If the addend is larger than the number you rounded to, you will need to add on a bit, to bring the sum up to the amount it would be if you used the non-rounded number. If the addend is smaller than the number you rounded to, you will need to subtract off the difference at the end. There are several ways you can record this thinking. Here are a few:
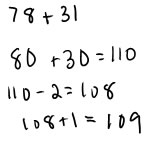 |
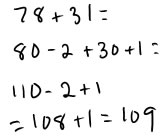 |
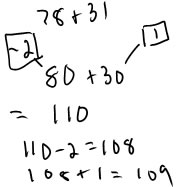 |
Some variations of this strategy involve rounding to the nearest 25: if numbers are close to a multiple of 25 (and you know your 25's from working with money), you can round to the nearest multiple of 25 and compensate; rounding just one number; or giving some from one number to the other to raise it to the nearest ten (using the make 10 strategy for 2 digit numbers).
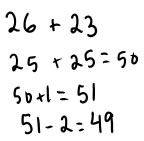 |
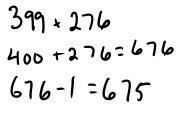 |
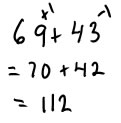 |
Algorithms from other countries:
In some other countries, there are slightly different standard algorithms. I don't know all of them, but the ones on the left is are used in various countries that were influenced by the British educational system (a very slight variation on our own--the "carried" digits are recorded in a different place), and the one on the right was used in India, though is no longer taught as a standard algorithm.
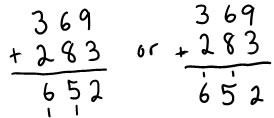 |
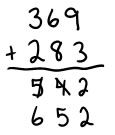 |
Universal, student invented algorithms:
One strategy that you often see when children are inventing ways to subtract is called the "negative numbers" algorithm. In this algorithm, you subtract as much as you can in each place value, using negative numbers to represent the amount left to be subtracted when the digit in the subtrahend is greater than the digit in the minuend. There are, of course, varying ways of representing this algorithm:
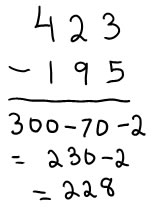 |
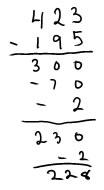 |
Think-out-loud: 400-100=300 20 minus 90 is negative 70 3 minus 5 is negative 2 300 - 70 = 280 |
Other think out loud: Take 100 from 400 leaves 300 |
Another common strategy that is significantly different from the standard algorithm is to subtract in each place value, going left to right. This is often represented as a set of subtraction problems as one might do if one were trying to solve the problem using a mental math strategy. This can also be represented as a subtraction in columns by crossing out digits where necessary, and it can include the same sorts of trading steps as the standard algorithm, though the order is quite different..
Mental math version:
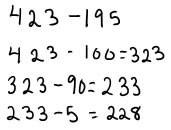
Version with trading (this often follows from a way of solving with base 10 materials)
|
Think out loud: First I take 100 away from 423, which leaves 323. |
Friendly numbers strategies (round and compensate):
Strategies that use rounding and then compensating are used most often when at least one number is near to a ten (for 2-digit problems) or near to a multiple of 100 (for 3 digit problems). Subtraction problems are trickier to solve this way than addition problems because the compensating strategy is different when you round in the subtrahend than when you round in the minuend.
If you round the number in the minuend, you can compensate in the same way that you do for addition: if you round up (from 598 to 600), then you have to compensate by subtracting the difference (2) at the end--the exact answer is 2 less than the rounded answer. If you round down (from 603 to 600) then you have to compensate by adding the difference (3) at the end--the exact answer is 3 more than the rounded answer.
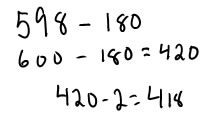 |
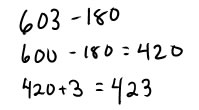 |
However, it works just the opposite way when you round the subtrahend: If you round up (from 298 to 300), then you have subtracted too much, so you have to add back the difference (2)--the exact answer is 2 more than the rounded answer. If you round down (from 302 to 300), then you haven't subtracted enough so you have to subtract the difference (2)--the exact answer is 2 less than the rounded answer.
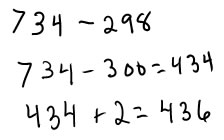 |
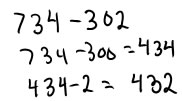 |
Alternate algorithms for teaching:
The main variation on the standard algorithm for subtraction that teachers would find it useful to introduce is to do all of the trading first before doing any of the subtractions. The reason this is sometimes a good variation to teach is because once the trading has been done it doesn't matter whether you subtract in columns right to left or left to right. Indeed, so long as care is taken to trade in fair ways (trade 100 for 10 tens and a ten for 10 ones), and that trades are only made for place values where they are needed, the trades can also be made either left to right or right to left.
For example--if you look at the first of these examples carefully, you'll see that the trade of 1 thousand for 10 hundreds was made before the trade of 1 hundred for 10 tens, which was made before the trade of 1 ten for 10 ones.
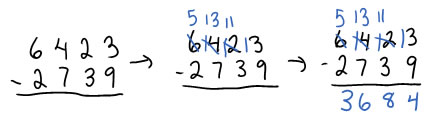
By comparison, in this example, the trade of 1 ten for 10 ones was made before the trade of 1 hundred for 10 tens, which happens before the trade of 1 thousand for 10 hundreds.
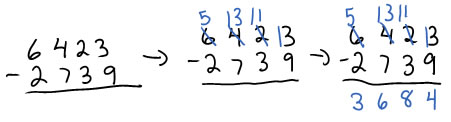
Algorithms from other countries:
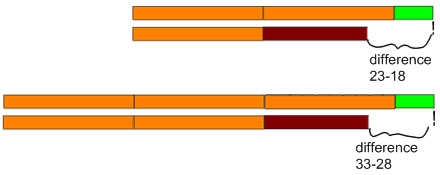
Unlike the addition algorithms, there is another common, very different, subtraction algorithm that is taught in some countries. I think if you surveyed countries, you would find that most of them teach the same standard algorithm than we do, but there are some (perhaps 25%) that have standardized on a significantly different algorithm. This algorithm is sometimes called the equal additions algorithm. In this algorithm, when we would normally trade a ten for 10 ones, instead you add equally to the minuend and the subtrahend.
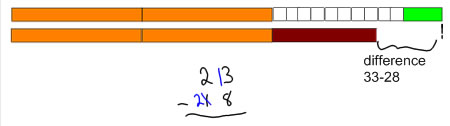
First you need to understand why this works: subtraction measures the difference between two numbers. If both numbers are increased by the same amount, then the difference stays the same:
Now, to to do this in a way that helps us subtract, we add the ten in different places: we add 1 ten to the subtrahend, and 10 ones to the minuend:
Here's a 3-digit example:
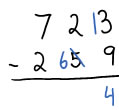 |
You can't take 9 from 3, so add 10 to the ones place of the minuend, so you have 13 ones. To keep the difference the same, add 10 in the tens place of the subtrahend so you have 6 tens. Subtract 9 from 13 to get 4. |
 |
You can't take 6 tens from 2 tens, so add 100 as 10 tens to the tens place of the minuend, so you have 12 tens. To keep the difference the same, add 100 to the hundreds place of the subtrahend so you have 3 hundreds. Take 6 tens from 12 tens to get 6 tens, and take 3 hundreds from 7 hundreds to get 4 hundreds. |
Now, this is probably pretty confusing to you right now, but if you try it out, you'll find that you can do it, and once you get used to it, you'll find it's easy enough to do. It turns out that once you understand this method and practice it, the algorithm is slightly easier and less problematic than the standard algorithm that we teach and learn in this country (students make fewer errors), but as you can see it's significantly harder to explain and understand--the trade off is that we have an algorithm that's slightly harder to do, but easier to understand. Because the difficulty difference is only a small one, I think we made the right choice for which algorithm to standardize to. I would not expect a child to invent this method spontaneously, but you might have a child in your class someday who learned this way of subtracting from a parent or grandparent, or in school if they had previously attended school in another country.