The traditional algorithm that we learned in school has some great advantages--it's compact (you can fit your work on a small amount of paper); it shows all of the important steps (you can look back later to see what you did at each step); it's thoroughly de-bugged (people have been using this for a long time, and there aren't any hidden problems with it) and it's what most people use (when someone else looks at your work they will know right away what you did and how you did it--no communication problems).
The traditional algorithm, however, doesn't always fit the way that children think. Using manipulatives to work through the steps helps make the standard algorithm make sense to children, but there are other approaches that have other advantages too. If you teach addition and subtraction through asking good problems and asking children to solve the problems in ways that make sense to them, children will come up with a range of strategies and ways of recording those strategies. Spending time developing childrens ideas is often time well spent in terms of children getting a robust understanding of how addition and subtraction works and what it represents. If you teach by questioning and problem solving you'll see a lot of different ideas and strategies that children come up with.
Even if you are teaching the traditional algorithm, there will be some children who come up with their own ways to add and subtract that work and make sense. It's important as a teacher to be able to look at work that children do, and recognize it as a valid alternate strategy that works and makes sense, or to recognize that it doesn't work, and figure out what the problem is with the strategy. It's discouraging for a child to use an alternate strategy that works (one they made up, or one they learned from a parent who grew up with a different school system) and be told that the they're wrong because they did it a different way. Even if we eventually want children to be able to all add and subtract using the standard algorithm, it's important to be able to recognize and praise correct thinking.
The other situation where learning other algorithms can be useful as a teacher is that there are some alternate ways of adding and subtraction that are sometimes used as a teaching strategy for children who aren't ready for the standard algorithms.
Universal student invented algorithms:
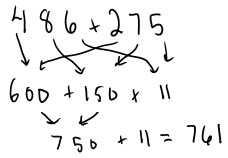
Universal algorithms for addition (efficient ones that use place value) always have some version of adding numbers in their place value, and then combining the numbers. The combining can be recorded in different ways and happen in different orders. Here are two examples:

Friendly numbers strategies:
Alternate algorithms for teaching: The expanded algorithm
Algorithms from other countries:
Universal student invented algorithms:
Friendly numbers strategies:
Alternate algorithms for teaching:
Algorithms from other countries: