More fractal ideas:
If an object is self similar, it's dimension can be defined in terms of how many copies of itself you need to build a new one that is bigger by a scale factor of 2. Your book explains this in section 6.6.
What you need to know is how scale factors and number of copies works with self similar figures, and what the patterns are for 1, and 2 dimensions:
If a self similar shape is 1-dimensional, then its scale factor and the number of copies you need are equal.
If a self similar shape is 2-dimensional then the number of copies you need is equal to the scale factor times itself.
| Scale Factor | # copies needed for 1D shape | # copies needed for 2D shape |
| 1 | 1 | 1 |
| 2 | 2 | 4 |
| 3 | 3 | 9 |
| 4 | 4 | 16 |
Practice question 1: If you have a self similar 2D shape where the scale factor comparing it to its smaller copies is 5, how many copies does it take to make the large 2D shape?
You may also find it useful to know that for a 0D shape, you only need 1 copy, no matter what the scale factor is, and for a 3D shape, you need to cube the scale factor to get the number of copies needed.
You need to be able to identify a fractal as being made of smaller similar copies, identify the scale factor and the number of copies needed to make the whole thing. You also need to be able to compare it with what happens for 1D and 2D shapes to say whether the shape is 1D, 2D, more, less, or somewhere in between. You don't need to know the logarithm formula from the book.
Practice questions:
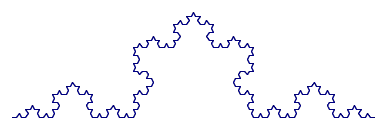
2. In this Koch curve, circle two pieces that are the same shape as the whole curve, but at a different magnification. For each of your pieces, tell how much (length scale factor) you would need to magnify them to get the whole thing, and how many of them it takes to make the whole thing:

3A. For the circled similar part of this Sierpinski triangle, tell the scale factor needed to enlarge it to the whole triangle, and the number of copies needed to create the whole triangle.
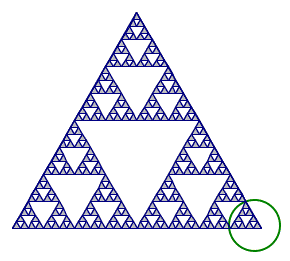
B. Compare the number of copies for this scale factor to the copies needed for a 1D and 2D shape. What does this tell about the fractal dimension of the Sierpinski triangle?
4A. For the smaller, similar part circled in this fractal, tell the scale factor to enlarge it to the larger whole curve, and the number of copies needed to create the larger whole curve.

B. Compare the number of copies for this scale factor to the copies needed for a 1D and 2D shape. What does this tell about the fractal dimension of this fractal?
5A. In this fractal, circle a piece that is the same shape as the whole curve, but smaller. For your circled piece, tell how much (length scale factor) you would need to magnify it to get the whole thing, and how many copies of it you need to make the whole thing:

B. Compare the number of copies for this scale factor to the copies needed for a 1D and 2D shape. What does this tell about the fractal dimension of the this fractal?
Also know: There are lots of objects in nature that are fractal-like. If they were exactly self similar, we could figure out their fractal dimension the way we do with the simple fractals. (Things in nature aren't exactly self-similar, and so mathematicians use counting tricks to compare area or length (how many copies you need) to scale factor to approximate a fractal dimension.). Take a look at some of these examples of fractals in nature, and be prepared to explain how you can see that these things are approximately self similar.