1. If I have a bag with 5 red and 3 blue marbles, and I pick two out (one and then the other,without replacing the first)

• What is the probability I will get two red marbles? P(RR) = (5/8)(4/7) = 20/56 = 5/14
• What is the probability I will get two blue marbles? P(BB) = (3/8)(2/7) = 6/56 = 3/28
• What is the probability that I will get one red and one blue? P(one of each) = 1-(5/14)-(3/28) = (56/56)-(20/56)-(6/56) = 30/56 = 15/28

For more details, or to make up a similar practice problem, see this page showing the work using multiplication, or this page showing the work using a tree diagram

2. The weatherman says that there is a 40% chance of rain tomorrow. What is the probability that it will not rain tomorrow?

P(no rain) = 100%-40% = 60%

3. In the same bag (above) with 5 red and 3 blue marbles, if I pick out three (without replacement)

• What is the probability I will get three red marbles? P(RRR) = (5/8)(4/7)(3/6) = 60/336 = 5/28
• What is the probability I will get at least one blue marble? P(at least 1 blue) = 1-(5/28)=(28/28)-(5/28) = 23/28
• What is the probability that I will get 3 blue marbles?
• What is the probability that I will get at least 1 red marble?

For more details, or to make up a similar practice problem, see this page showing the work using multiplication and subtraction.

4. In a bag with 6 green and 5 yellow marbles, I pick 3 without replacement.

Using the diagram below, answer:

• What is the probability I will get at least 2 yellow: add probabilities shown in orange and red below: (120/990)+(120/990)+(120/990)+(60/990) = 420/990 = 14/33
• What is the probability I will get exactly 2 yellow: add probabilities shown in orange below: (120/990)+(120/990)+(120/990) = 360/990 = 4/11
• What is the probability I will get at least 2 green: add probabilities shown in black below: (120/990)+(150/990)+(150/990)+(150/990) = 570/990 = 19/33

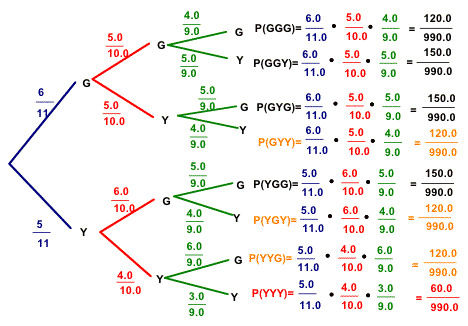
To make up a similar practice problem see here